CIRCUITOS SECUENCIALES

En la siguiente entrada vamos a proceder a realizar una breve introducción acerca de los circuitos secuenciales.

Los circuitos secuenciales se caracterizan porque las variables de salida, en un determinado instante, dependen de las variables de entrada en ese mismo instante y de la historia del circuito (los estados anteriores por los que haya pasado).

Son, por tanto, sistemas capaces de memorizar cierta información de lo sucedido con anterioridad a un determinado momento (historia pasada por el circuito), y utilizar esta información conjuntamente con una combinación lógica de sus entradas de datos para determinar el futuro estado del sistema.

Muchos de los sistemas digitales prácticos se realizan siguiendo la filosofía de los circuitos secuenciales (circuitos de control, sistemas de alarma y seguridad, relojes, etc.).

La estructura general de un circuito secuencial responde al diagrama de bloques del modelo Huffman:

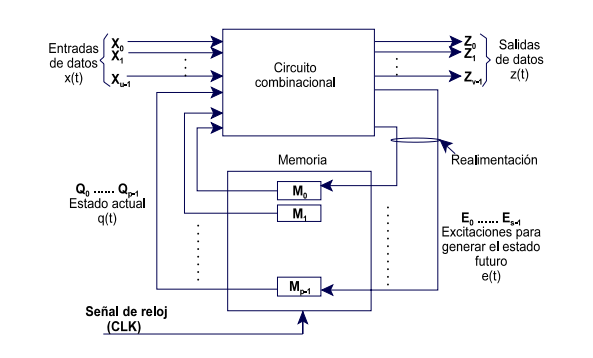Modelo Huffman

Los sistemas secuenciales se pueden clasificar en dos grandes bloques: síncronos y asíncronos.

Esta clasificación se hace atendiendo a los tipos de elementos de memoria utilizados. La diferencia entre los sistemas secuenciales síncronos y asíncronos está en que en los primeros los cambios de estado son controlados por una señal de referencia común (señal de reloj) y los segundos no.

En un circuito secuencial asíncrono ante un cambio en las señales de entrada de datos, las salidas alcanzarán sus niveles definitivos, transcurrido un tiempo que será función de los tiempos de propagación del circuito combinacional y de los elementos de memoria (en realidad las salidas de datos se estabilizarán cuando se estabilicen las salidas de los elementos de memoria).

Tiempos estos que pueden variar entre un valor mínimo y un máximo, y que por tanto introducen un cierto grado de incertidumbre en los tiempos que tardan en propagarse los cambios de las variables de entrada a sus salidas. Hay que advertir que pueden existir situaciones en las que no se alcance la estabilidad (estados metaestables).

Según esto, en los circuitos secuenciales asíncronos después de producirse un cambio en las entradas hay que esperar un tiempo hasta que se estabilicen los valores de las salidas y sólo después de que se alcance esta estabilización se podrá realizar otro cambio en sus entradas, ya que en caso contrario no se verán reflejados en las salidas estos cambios. Evidentemente, el tiempo mínimo entre dos cambios consecutivos en las entradas de datos es función de los tiempos de propagación del circuito combinacional y elementos de memoria.

El gran inconveniente de los circuitos asíncronos es que la incertidumbre de los tiempos de propagación se traduce en incertidumbres en el cambio de las señales de salida.

Los circuitos síncronos lo que hacen es eliminar esta incertidumbre utilizando una señal de sincronismo o señal de reloj. La señal de reloj lo que hace es permitir que los cambios en las entradas y en los estados internos tengan efecto sobre el resto del sistema sólo en instantes discretos de tiempo.

Estos instantes discretos suelen coincidir con los flancos de subida o bajada de la señal de reloj. Así, la salida que adopten los elementos de memoria, después de un flanco de reloj (CLK), será función únicamente de los valores que tenían sus entradas en el instante anterior al flanco de CLK.

Actualmente existe un auge e interés por el diseño de circuitos VLSI asíncronos o autotemporizados, ya que el aumento de velocidad de operación y la complejidad de los circuitos digitales conllevan grandes problemas para conseguir que las señales de reloj que se propaguen por caminos diferentes tengan idénticos tiempos de propagación. Esto hace que la distribución de la señal de reloj dentro de los circuitos digitales sea una tarea compleja, siendo una de las razones de esta complejidad los retrasos en la señal de reloj (lo que se conoce como clock skew), además de los problemas de interferencias que puede sufrir la señal de reloj (cross-talk).

Representación de los automatas.

Las dos realizaciones básicas de los autómatas finitos son las máquinas de Mealy y de Moore, que a su vez, pueden ser síncronas o asíncronas.

Para representar el comportamiento de los circuitos secuenciales se utilizan:

Tablas de estados o tablas de transición (en un formato similar a las tablas de verdad).

Grafos (también conocidos como diagramas de estados), donde aparecen los diferentes estados (que son finitos) y las funciones de transición de las salidas para cada combinación de las entradas (que también son finitas).

Estas tablas y grafos difieren dependiendo de si se trata de un autómata o máquina de Mealy o de Moore.

Toda máquina mealy se puede transformar en una máquina Moore y viceversa

Automata de Mealy.

En una máquina Mealy, las salidas pueden cambiar si cambian las entradas y ello sin necesidad de que se produzca un pulso en el bloque de registros.

En este tipo de representación los estados se muestran dentro de círculos. La transición entre estados se indica con arcos que conectan dos estados y sobre estos arcos se indica la entrada que provoca la transición y la salida para esa entrada y el estado actual.

Diagrama de flujo.

Automata de Moore.

La máquina Moore es un caso particular de máquina Mealy, en la que las salidas dependen exclusivamente del estado interno y no de las entradas.

Por ello, en una máquina Moore, si alguna entrada cambia, las salidas no cambian al menos hasta que no aparezca un pulso de reloj que origine un cambio en los estados internos (elementos de memoria). Un ejemplo de máquina Moore lo constituye un contador.

Grafos (diagramas de flujo)

En este tipo de representación los estados y salidas actuales se muestran dentro de círculos. La transición entre estados se indica con arcos que conectan dos estados y sobre estos arcos se indica la entrada que provoca la transición.